a can factory requires 2 sheets of metal The proportionality constant between the number of cans made and the number of sheets of metal used is Your solution’s ready to go! Our expert help has broken down your problem into an . Gauge. Stainless. Galvanized. Sheet Steel . 0.0703 (1.8) 0.0710 (1.80) 0.0673 (1.71) 0.0571 (1.4) 14. 5/64. 0.0751 (1.9075) 0.0785 (1.99) 0.0747 (1.90) 0.0641 (1.63) 13. 3/32. 0.0900 (2.286) 0.0934 (2.37) 0.0897 (2.28)
0 · can factory requires 2 sheets of metal to make 36 cans 10 sheets
1 · Solved: A can factory requires 2 sheets of metal to make 36 cans
2 · Solved A can factory requires 2 sheets of metal to make 36
3 · Select the correct answer from the drop
4 · Select the Correct Answer from the Drop
5 · Acan factory requires 2 sheets of metal to make 36 cans and 10
6 · A can factory requires 2 sheets of metal to make 36 cans and 10
7 · A can factory requires 2 sheets of metal to make 36 cans and
8 · A can factory requires 2 sheets of metal to
9 · A Can Factory Requires 2 Sheets of Metal
Always use a higher argon-based shielding gas, such as 75% argon/25% carbon dioxide. Argon carries less heat than pure CO2, and you’ll experience less spatter. When .
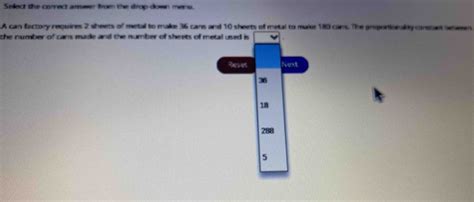
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of .
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans The proportionality constant between the number of cans made and the number of .Answer: 1 sheet of metal is equivalent to 18 cans. Step-by-step explanation: If you divide 36/2 you get 18 and if you divide 180/10 you also get 18. So the proportionality of cans made to the .
Divide the number of cans by the number of sheets to find the constant. 36 cans / 2 sheets = 18 cans per sheet. 180 cans / 10 sheets = 18 cans per sheet. The proportionality constant is 18 .
The proportionality constant between the number of cans made and the number of sheets of metal used is Your solution’s ready to go! Our expert help has broken down your problem into an .A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used is Reset Next 36 18 288 5. . let y = # of sheets. x = # of cans. y = kx where k is the proportionality constant. Assuming linear relationship of the two, we can use either data point as follows: y = kx. 2 = .Acan factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. the proportionality constant between the number of cans made and the number of .
For 2 sheets of metal: Proportionality constant = Number of cans / Number of sheets = 36 / 2 = 18. For 10 sheets of metal: Proportionality constant = Number of cans / Number of sheets = 180 / . To solve for the proportionality constant, we can set up a ratio. As given in the question, 2 sheets of metal produce 36 cans, so we can write this ratio as 36 cans / 2 sheets of metal which simplifies to 18 cans per sheet of metal. This tells us that the proportionality constant is .
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used is
can factory requires 2 sheets of metal to make 36 cans 10 sheets
Solved: A can factory requires 2 sheets of metal to make 36 cans
brainerd stainless steel cabinet pulls
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans The proportionality constant between the number of cans made and the number of sheets of metal used is squareAnswer: 1 sheet of metal is equivalent to 18 cans. Step-by-step explanation: If you divide 36/2 you get 18 and if you divide 180/10 you also get 18. So the proportionality of cans made to the number of sheets of metal used would be 1:18Divide the number of cans by the number of sheets to find the constant. 36 cans / 2 sheets = 18 cans per sheet. 180 cans / 10 sheets = 18 cans per sheet. The proportionality constant is 18 cans per sheet.
The proportionality constant between the number of cans made and the number of sheets of metal used is Your solution’s ready to go! Our expert help has broken down your problem into an easy-to-learn solution you can count on.A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used is Reset Next 36 18 288 5. Click here 👆 to get an answer to your question ️ Select the correct answer from the drop-down menu. let y = # of sheets. x = # of cans. y = kx where k is the proportionality constant. Assuming linear relationship of the two, we can use either data point as follows: y = kx. 2 = k(36) k = 1/18. Therefore, the proportionality constant is 1/18.
Acan factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. the proportionality constant between the number of cans made and the number of sheets of metal used is Answers: 2For 2 sheets of metal: Proportionality constant = Number of cans / Number of sheets = 36 / 2 = 18. For 10 sheets of metal: Proportionality constant = Number of cans / Number of sheets = 180 / 10 = 18. Both calculations yield the same proportionality constant, confirming the consistency.
To solve for the proportionality constant, we can set up a ratio. As given in the question, 2 sheets of metal produce 36 cans, so we can write this ratio as 36 cans / 2 sheets of metal which simplifies to 18 cans per sheet of metal. This tells us that the proportionality constant is .
A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used isA can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans The proportionality constant between the number of cans made and the number of sheets of metal used is squareAnswer: 1 sheet of metal is equivalent to 18 cans. Step-by-step explanation: If you divide 36/2 you get 18 and if you divide 180/10 you also get 18. So the proportionality of cans made to the number of sheets of metal used would be 1:18
Divide the number of cans by the number of sheets to find the constant. 36 cans / 2 sheets = 18 cans per sheet. 180 cans / 10 sheets = 18 cans per sheet. The proportionality constant is 18 cans per sheet.The proportionality constant between the number of cans made and the number of sheets of metal used is Your solution’s ready to go! Our expert help has broken down your problem into an easy-to-learn solution you can count on.A can factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. The proportionality constant between the number of cans made and the number of sheets of metal used is Reset Next 36 18 288 5. Click here 👆 to get an answer to your question ️ Select the correct answer from the drop-down menu. let y = # of sheets. x = # of cans. y = kx where k is the proportionality constant. Assuming linear relationship of the two, we can use either data point as follows: y = kx. 2 = k(36) k = 1/18. Therefore, the proportionality constant is 1/18.
Acan factory requires 2 sheets of metal to make 36 cans and 10 sheets of metal to make 180 cans. the proportionality constant between the number of cans made and the number of sheets of metal used is Answers: 2
brake line junction box pontiac montana youtube
Solved A can factory requires 2 sheets of metal to make 36
Apart from few Russian repack groups Blackbox, CorePack and FitGirl are still continuing to repack games. blackboxrepack.com.
a can factory requires 2 sheets of metal|Select the correct answer from the drop