what does a normal distribution box plot look like One way to understand a box plot is to think of what a box plot of data from a normal distribution will look like. The graph below shows a standard normal probability density function ruled into four quartiles, and the box plot you would .
Different people (Engineers & Electricians) give me different answers on this, but who is really right? My question is - can two NM cables be pulled into one knockout in a metal 1900 box? This is a standard 4" box with the preinstalled clamps, two .
0 · skewed to the right boxplot
1 · positively skewed distribution box plot
2 · positively skewed box plots
3 · positive skew vs negative boxplot
4 · how to interpret boxplot results
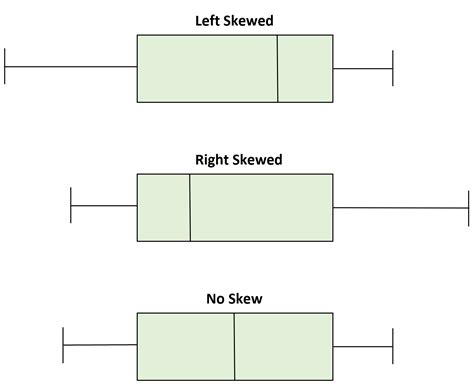
5 · boxplot skewed to the left
6 · box and whiskers chart explained
7 · 25th percentile on a boxplot
Wilton Metal Box Company (Pvt) Ltd - Piliyandala . Contact; Overview; Reviews; Photos +94112614731 +94112614308 +94112606952 +94112613857 [email protected] (142/2, .
skewed to the right boxplot
What is a Box Plot? A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset. A box plot . A boxplot, also known as a box plot, box plots, or box-and-whisker plot, is a standardized way of displaying the distribution of a data set based on its five-number summary .A box plot (aka box and whisker plot) uses boxes and lines to depict the distributions of one or more groups of numeric data. Box limits indicate the range of the central 50% of the data, with .
Review of box plots, including how to create and interpret them.
A box plot shows the distribution of data for a continuous variable. How are box plots used? Box plots help you see the center and spread of data. You can also use them as a visual tool to check for normality or to identify .
One way to understand a box plot is to think of what a box plot of data from a normal distribution will look like. The graph below shows a standard normal probability density function ruled into four quartiles, and the box plot you would .Histogram, boxplot and normal probability (Q-Q) plot are popular graphs used to explore the distribution of data. If the data are taken from a normal population, the histogram should .v. t. e. A normal distribution or Gaussian distribution (also known as the "bell-shaped curve") is a concept used in probability theory and statistics. [2] The normal distribution concept is applied in numerous disciplines, including .
The box plot (a.k.a. box and whisker diagram) is a standardized way of displaying the distribution of data based on the five number summary: minimum, first quartile, median, third quartile, and .
This video points out the possible connection between a symmetric box and whisker plot and the normal distribution.It has a different use. Normally I'd overlay a normal distribution on a histogram. A box plot can be used to compare data that aren't normally distributed. The intent behind box plots is to get an idea of where most of the data are and visualize if some data are quite far away, depending on how the whiskers are determined.
Which method of the three: histogram, box plot and probability plot is best at determining whether a distribution is approximately normally distributed? Why? If I were to plot the probabilities for a normal distribution what would the boxplot looks like? Would it always be symmetric for every parameter value? . a symmetric boxplot that the median is at the midpoint between the lower and upper quartile (i.e., in the middle of the box) .The standard normal probability (Q-Q) plot is on the left. The detrended normal Q-Q plot on the right shows a horizontal line representing what would be expected for that value if the data sere normally distributed. Any values below or above represent . A box plot is a type of plot that displays the five number summary of a dataset, which includes: The minimum value; The first quartile (the 25th percentile) The median value; The third quartile (the 75th percentile) The maximum value; We use the following process to draw a box plot: Draw a box from the first quartile (Q1) to the third quartile (Q3)
N.B. several variants of box plots exist; authors are often poor at documenting the precise rules used by their software. The popularity of the box plot has its price. Box plots can be very useful for showing the gross features of many groups or . The data may look like it follows a normal distribution when presented in a box plot, but it might be something else entirely. . everything looks like a nail”. Box plots should be used in .
positively skewed distribution box plot
Like @Glen_b said, you can compare your data with the data you're sure is normal - the data you generated yourself, and then rely on your gut feeling :) The following is an example from OpenIntro Statistics textbook. Let's have a look at this Q-Q Plot: Is it normal? Let's compare it with normally distributed data:The box plot is the graphical representation of the collected sample. The box plot is used to describe the distribution of the sample. To make this plot, first, we need to obtain the first quartile, the third quartile, the median, and the whiskers.$\begingroup$ Tukey's Three-Point Method works very well for using Q-Q plots to help you identify ways to re-express a variable in a way that makes it approximately normal. For instance, picking the penultimate points in the tails and the middle point in this graphic (which I estimate to be $(-1.5,2)$, $(1.5,220)$, and $(0,70)$), you will easily find that the square root comes close .The box plot is the graphical representation of the collected sample. The box plot is used to describe the distribution of the sample. To make this plot, first, we need to obtain the first quartile, the third quartile, the median, and the whiskers.
The box plot will look as if the box was shifted to the left so that the right tail will be longer, and the median will be closer to the left line of the box in the box plot. If the distribution is skewed to the left, most values are 'large', but there are a few exceptionally small ones.
Outlier : If a value is higher than Q3 + 1.5*(Q3-Q1), the value will be considered as outlier.Similarly, if a value is lower than Q1 - 1.5*(Q3-Q1), the value will be considered as outlier.Here Q1 and Q3 are first and third quartile. Normal Distribution : If a box plot has equal proportions around the median, we can say distribution is symmetric or normal.For example, the normal probability Q-Q plot below displays a dataset with 5000 observations along with the normality test results. The p-value for the test is 0.010, which indicates that the data do not follow the normal distribution. . In regression analysis, a residual plot is a type of plot that displays the fitted values of a regression model on the x-axis and the residuals of the model along the y-axis. When visually inspecting a residual plot, there are two . The problem with the box plot is you have no reference distribution against which to compare your sample, so little way of assessing normality. The Q-Q plot is much better suited to this purpose. Or you could compare a .
Use a histogram, KDE plot, or something for a better look at the distribution, not the quartiles. This looks heavily skewed. Could assume lognormal distribution, but depending on the data, could even be exponential (waiting times), etc. $\begingroup$ It's a relatively simple multiple and it results in an expected outlier rate of just under 1% for Normal distributions. If it were changed to 2.0, the rate would drop to 0.07% and if it were set only at 1.0, the rate would soar to over 4%. Since Tukey used boxplots to analyze smallish batches of data (comprising five to a few hundred values), a rate of 1% would .
Learn more about box plot, distribution . . However, if you find the best fit for the distribution (which is most probably not a normal distribution due to the skewness) the median will be different. pd=fitdist(x, 'Normal') h = chi2gof . If you'd like to use a boxplot for other reasons, note that you could compute the expected value from . I'm trying to plot box plots with normal distribution of the underlying data next to the plots in a vertical format like this: This is what I currently have graphed from an excel sheet uploaded to R: And the code associated with them:The residual series looks like: The residual series pass the Ljung Box test with a p value 0.3859. The ACF and PACF of the residual series are as follows (seems it is uncorrelated, right?): . The QQ plot does not look good, it shows fatter tails than a normal distribution would have. You can test normality assumption using a number of tests .

The normal distribution is the most commonly used probability distribution in statistics.. It has the following properties: Symmetrical; Bell-shaped; If we create a plot of the normal distribution, it will look something like this: The uniform distribution is a probability distribution in which every value between an interval from a to b is equally likely to occur.
Symmetry or not. The plot for the nearly normal distribution (Figure 8) shows symmetry, while the plot for the non-normal distribution (Figure 9) does not. Mean and median nearly equal. In these box plots, the horizontal black center line in the box is the median, and the blue line is the mean.
There is a simpler answer to this. If your data came from a Likert scale, they cannot be normally distributed. The normal distribution goes to infinity in both directions. Likert scales are finite. The normal distribution can take any fractional value. A Likert scale cannot have infinite possible values in between the response options. Key Points on Q-Q Plots. Quantile-Quantile (Q-Q) Plots compare the distribution of two sets of data. They are especially useful for comparing a data set to a theoretical distribution, often the standard normal distribution. `qqnorm()` Function in R compares data to the theoretical normal distribution and plots a straight line if the quantiles . A Q-Q plot, short for “quantile-quantile” plot, is used to assess whether or not a set of data potentially came from some theoretical distribution.. In most cases, this type of plot is used to determine whether or not a set of data follows a normal distribution. As a rule of thumb, the more that the points in a Q-Q plot lie on a straight diagonal line, the more normally distributed .
$10.99
what does a normal distribution box plot look like|25th percentile on a boxplot